Additive Synthese

Nachdem in der ersten Folge über Synthesizer die Grundlagen der Klangsynthese erarbeitet wurden, geht es heute ans Eingemachte: Wir starten mit der Additiven Synthese.

Wir erinnern uns: Eine beliebige Wellenform kann durch die Summe mehrerer Sinus- und Cosinus-Schwingungen unterschiedlicher Frequenz und Amplitude dargestellt werden (in der Musik spricht man meist von Harmonischen und meint damit Sinus-Schwingungen; aus mathematischer Sicht ist das etwas Wischiwaschi, darauf gehe ich in der nächsten Folge ein.).

Nach dem Fourier-Theorem reicht es aus, wenn die einzelnen Frequenzen ganzzahlige Vielfacheeiner Grundfrequenz sind. Das ist ein Glück für uns, denn somit müssen wir nicht mehr unendlichviele, sondern unter Umständen nur noch verdammtviele Harmonische berücksichtigen.

Additive Synthese – Ein bisschen Historie

Nicht das erste, aber eines der bekanntesten Instrumente, welches diesen Umstand ausnutzt und eigentlich mit der additiven Synthese arbeitet, ist die Hammond B3 – das gilt natürlich auch für verwandte Orgelmodelle plus ungezählte Klone, die auf Zugriegel oder Chöresetzen.

Bei der B3 wird die Wellenform des Orgelklanges aus neun Harmonischen „zusammengebaut“. Jeder Harmonischen ist wiederum ein Zugriegel zugeordnet, welcher die Lautstärke (Amplitude) der Harmonischen in neun Abstufungen von „0“ (Stille) bis „8“ (volle Pulle) bestimmt.

Die neun Zugriegel eines Hammond-B3-Klons (hier: Roland VK-8).
Beschriftung und Anordnung sind durchaus gewöhnungsbedürftig.

Allerdings erkennt man nicht auf den ersten Blick, welche Harmonische da von welchem Zugriegel bedient wird, denn die Beschriftungen der Riegel sind doch recht merkwürdig. Das soll uns aber nicht stören; Interessierte mögen die folgende gelbe Box zu Rate ziehen.

Die Beschriftung der Zugriegel leitet sich von der guten alten Kirchenorgel ab: Mit einer 8‘ (acht Fuß = 2,44 Meter) langen Orgelpfeife erzeugt man das tiefe C; dies definiert auch die Grundfrequenz. Ein 4‘-Pfeife erzeugt die doppelteFrequenz einer 8‘-Pfeife, eine 2 2/3‘-Pfeife die dreifache Frequenz usw.

Offenbar gelang es den Orgelbauern eines Tages, auch längere Pfeifen zu bauen. Jedenfalls kam die 16‘-Pfeife dazu, die mit der halben Grundfrequenz hupt. Und zu allem Unglück hat man noch die 5 1/3‘-Pfeife mit der anderthalbfachen Grundfrequenz dazu gebastelt. Das Schlamassel klärt sich aber auf, wenn wir anstelle der 8‘ ganz frech die 16‘ als Grundfrequenz erklären, denn dann erhalten wir folgendes Muster:

Fußlage	Frequenz
16‘	1 x Grundfrequenz
8‘	2 x Grundfrequenz
5 1/3‘	3 x Grundfrequenz
4‘	4 x Grundfrequenz
2 2/3‘	6 x Grundfrequenz
2‘	8 x Grundfrequenz
1 3/5‘	10 x Grundfrequenz
1 1/3‘	12 x Grundfrequenz
1	16 x Grundfrequenz

Na bitte. Man sieht, dass in dieser Reihe die Harmonischen mit der fünf- und siebenfachen Grundfrequenz etc. nicht mit von der Partie sind. Diese Auswahl hat neben der „harmonischen Qualität“ sicher auch historische Gründe – und irgendwie muss man sich ja bei nur neun Harmonischen entscheiden.

Schön und gut, aber wie klingt das jetzt? Dazu bedienen wir uns des folgenden Klangbeispiels. Man hört zunächst die einzelnen Harmonischen von 16‘ bis 1‘ (also in der „logischen“ Reihenfolge 16‘, 8‘, 5 1/3‘, 4‘ …), und danach alle zusammen, wobei eine Harmonische nach der anderen hinzukommt. Man beachte außerdem die Abstufungen der Lautstärke, wenn die einzelnen Zugriegel gezogen werden.

Additive Synthese – Hüllen für den Klang

Ein Problem der Orgeln allgemein – und eben auch der Hammond-Artigen – ist, dass sie doch ziemlich statisch klingen. Es gibt nämlich keine Möglichkeit, die Lautstärke der einzelnen Harmonischen zu modulieren(es sein denn, man zieht während des Spielens an den Zugriegeln). Man kennt das vom klassischen Analogsynthesizer: Hier kann beispielsweise der LFO oder der ADSR-Generator die Eckfrequenz des Filters steuern, was zu interessanten dynamischen Klangänderungen führt. Orgeln besitzen zwar meist ein 4‘- bzw. 2 2/3‘-Percussion-Register, der Effekt ist aber wahrlich nicht vergleichbar. Man müsste die einzelnen Harmonischen selbst mit eigenen Hüllkurvenversehen können, welche dann zeitabhängig deren Amplituden kontrollieren.

Moment, jetzt erst mal einen Schritt zurück: Was genau ist eine „Hüllkurve“ (englisch: Envelope)? Damit meint man einfach einen Wert, der sich in der Regel ab einem bestimmten Startzeitpunkt verändert (oder auch nicht) und die Variation (Modulation) der Lautstärke, der Frequenz etc. beschreibt. Typisches Beispiel: Bei einem Klavierklang nimmt die Lautstärke nach dem Tastenanschlag allmählich ab, bis der Ton ganz verklingt. Die Hüllkurve der Lautstärke besitzt also zu Beginn einen sehr hohen und mit fortlaufender Zeit abfallenden Wert. Anderes Beispiel: Flöte. Hier steigt die Hüllkurve der Lautstärke zunächst schnell an, um dann solange auf einem mehr oder weniger konstanten Wert zu bleiben, bis der Flötenton abbricht.

Praktisch alle Synthesizer haben einen oder mehrere Module (Generatoren), die solche Hüllkurven „erzeugen“. Wird der Generator z. B. bei einem Tastendruck gestartet, dann produziert er anhand eines vorgeschriebenen Schemas fortlaufend und automatisch Hüllkurven-Werte, die wiederum zur Modulation der Lautstärke etc. verwendet werden können. So ein Generator bringt Schwung ins Spiel und belebt den Klang ganz ungemein, vor allem, wenn er nicht nur zur Variation der Lautstärke, sondern auch der Klangfarbe selbst herangezogen wird.

Additive Synthese – Die 3½-te Dimension

Genau das hat man sich z. B. beim Fairlight CMI(bzw. schon bei dessen Vorgänger, dem Quasar M8, später dann auch beim NED Synclavierund dem PPG Waveterm) gedacht. Nun ist der Fairlight eigentlich eher für sein revolutionäres Sampling bekannt, d. h. die Möglichkeit, ein Tonsignal digital aufzuzeichnen und dann in nahezu beliebiger Tonhöhe wieder abzuspielen. Der Fairlight ist aber im Wesentlichen auch ein Computer, und additive Synthese geht mit Computern ganz gut zusammen. Warum also nicht gleich das Tonsignal berechnen, anstatt es aufzunehmen?

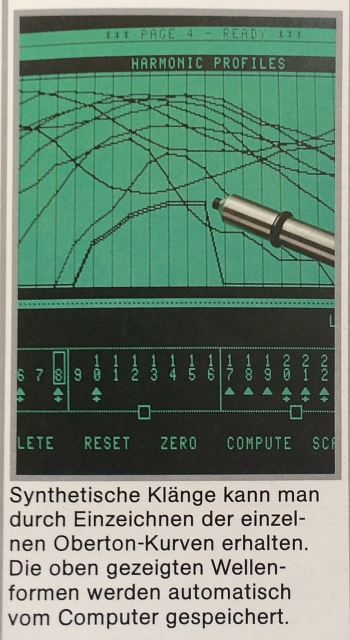
Tatsächlich hat man beim Fairlight (genauer gesagt beim Fairlight CMI Series II) die Möglichkeit, die Hüllkurven der Amplituden von 32 Harmonischen in 32 Schritten zu beeinflussen. Mithilfe eines Lichtgriffels können auf der Page 4, einer besonderen Bildschirmseite des Fairlights, diese Hüllkurven „gemalt“ werden. Der Computer berechnet dann anhand der Hüllkurvenwerte die jeweiligen Summen der Harmonischen und schreibt die sich ergebenden Klangdaten in den Speicher. Jetzt kann man das additiv synthetisierte Klanggebilde wie ein normales Sample spielen. Oder man schaut sich die harmonischen Profile hintereinander gestaffelt als „Wellengebirge“ auf der Page Dan.

Die Sache hat natürlich einen Haken: Ist der Klang erst einmal erstellt, kann man ihn in Echtzeit nicht mehr verändern – dazu müsste er immer wieder neu berechnet werden, und das schafft der Fairlight nicht, der Rechner ist einfach zu lahm. Deshalb auch die merkwürdige Überschrift dieses Abschnitts, für eine ganze vierte Dimension der Zeit reicht es leider nicht.

Die wirklich dynamische Echtzeit-Kontrolle der Harmonischen kam (in bezahlbarer Form) erst 1987 mit dem Kawai K5 und später (1996) mit dem K5000 in die Läden. Durch geschicktes Gruppieren und gemeinsames Modulieren der Harmonischen kann hier die Flut an möglichen Parametern in Grenzen gehalten werden. Richtig durchgesetzt haben sich diese wegweisenden Synthesizer aber irgendwie nicht. Schade.

Additive Synthese – Back to the Future

Zurück zum Thema! Man würde doch sehr gerne mal selbst ausprobieren, wie sich additive Synthese bei Fairlight und Konsorten (NED Synclavier, PPG Waveterm usw.) so anfühlt. Leider ist heutzutage weniger der Preis als schlichtweg die geringe Verfügbarkeit der alten Boliden das größte Hindernis für ein solches Unterfangen. Doch zum Glück gibt es ja Software, welche diese Geräte zumindest teilweise emuliert. Meine Lieblings-Weichware istAudio-Term, ein kostenloses Windows-Programm von Mathias Gurk. Man muss ein bisschen im Internetz stöbern, bis man das gute Stück findet; relativ stabil sollte der folgende Link sein: http://www.wusik.com/download/AudioTerm.html

Das Schöne an Audio-Term ist, dass man gleich die (aus heutiger Sicht) seltsam anmutende Benutzeroberfläche mit dazu bekommt – echt retro.

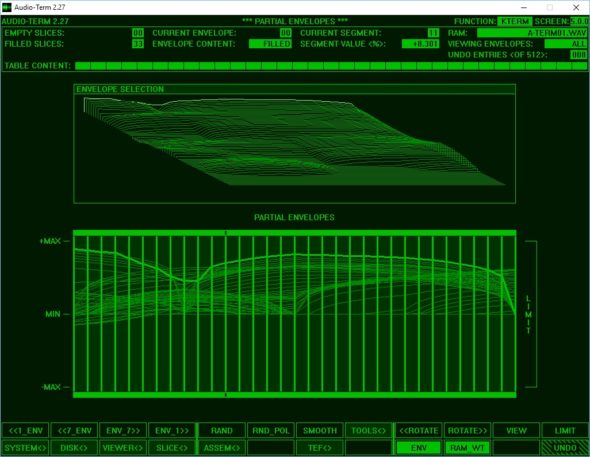
Additive Synthese betreiben kann man im Audio-Term-Modul KTERM(der Menüpunkt heißt aus gutem Grund übrigens „Wavetable Synthesis“). Sehen wir uns dort mal die Partial Envelopes-Seite an: Hier lässt sich für jede Harmonische (Partial) der Lautstärkeverlauf über die Zeit zeichnen – allerdings mit der Maus, Lichtgriffel sind irgendwie out.

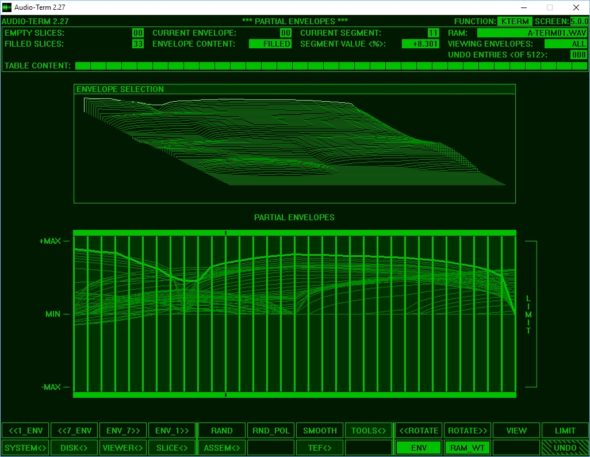
Alternativ ändert man die Amplituden aller Harmonischen gleichzeitig im Slice Editor. Ein Sliceist so etwas wie ein Schnappschuss zu einem bestimmten Zeitpunkt; KTERMbietet, wie der alte Fairlight, 32 Stück davon. Die Slices dienen als Stützpunkte zur Berechnung (besser: Interpolation) der eigentlichen Hüllkurven. Wenn man ein Slice erstellt, sieht man im Fenster auch gleich die Wellenform, die sich daraus ergibt. Und über die Funktion „WDRAW“ kann man die Wellenform sogar selbst zeichnen.

Man beachte, dass Audio-Term nur Sinus-Schwingungen zur Berechnung der Wellenformen heranzieht – der Cosinus bleibt außen vor. Das hat unter anderem die Konsequenz, dass die „rechte Hälfte“ einer generierten Wellenform immer dem Spiegelbild der „linken Hälfte“ entspricht, allerdings „auf den Kopf“ gestellt. Man kann also nicht jede beliebige Wellenform erzeugen; mehr dazu in der nächsten Folge.

Viel Spaß beim Lesen!

Zum Abschluss habe ich drei kleine, unspektakuläre Klangbeispiele mit Audio-Term gebastelt. Im ersten Beispiel hört man, wie nach und nach von der ersten bis zur zehnten Harmonischen überblendet wird:

Im zweiten Beispiel erklingt ein immer dumpfer werdender Sägezahn mit pieksigem Ende:

Das dritte Beispiel ergab sich einfach so durch Rumspielen:

Additive Synthese – Aussicht

Additive Synthese ist ein Klassiker und erlaubt es, einen Klang von Grund auf zusammenzubauen. Das ist nicht besonders kompliziert, kann allerdings sehr komplexwerden (Viele, viele Hüllkurven sind zu zeichnen!). Vermutlich gibt es deshalb auch nur relativ wenige Instrumente, die auf Additive Synthese setzen, und das gilt nicht nur für die Hardware: „Additive“ machen nur einen kleinen Teil der schier unüberschaubaren Anzahl von Software-Synthesizern aus.

In der Einleitung habe ich schon angedeutet, dass der Begriff der Harmonischen nicht ganz unproblematisch ist. Darauf gehe ich in der nächsten Folge genauer ein und wage dann den Übergang zu den „natürlichen Verwandten“ der additiven Synthese.